Good day.
I've been trying to simulate a aluminum circle immersed in water with 'pstdElastic2D' in order to see the behavior of an ultrasonic signal passing through it. I have used the following code for simulation:
clc
clear all
close all
% =========================================================================
% SIMULATION PARAMETERS
% =========================================================================
% change scale to 2 to reproduce the higher resolution figures used in the
% help file
scale = 1;
% create the computational grid
PML_size = 10*scale; % size of the PML in grid points
Nx = 220*scale - 2*PML_size; % number of grid points in the x direction
Ny = 220*scale - 2*PML_size; % number of grid points in the y direction
dx = 0.1e-3/scale; % grid point spacing in the x direction [m]
dy = 0.1e-3/scale; % grid point spacing in the y direction [m]
kgrid = makeGrid(Nx, dx, Ny, dy);
% define the medium properties
% === WATER
cp1 = 1480; % compressional wave speed [m/s], 1540 === 1480
cs1 = 0; % shear wave speed [m/s]
rho1 = 1000; % density [kg/m^3]
alpha0_p1 = 0.0; % compressional wave absorption [dB/(MHz^2 cm)]
alpha0_s1 = 0.0; % shear wave absorption [dB/(MHz^2 cm)]
% === ALUMINUM
cp2 = 6320; % compressional wave speed [m/s], 3000 === 6320
cs2 = 3100; % shear wave speed [m/s], 1400 === 3772
rho2 = 2720; % density [kg/m^3], 1850
alpha0_p2 = 1; % compressional wave absorption [dB/(MHz^2 cm)]
alpha0_s2 = 1; % shear wave absorption [dB/(MHz^2 cm)]
% create the time array
cfl = 0.1;
t_end = 15e-6;
kgrid.t_array= makeTime(kgrid, cp2, cfl, t_end);
% define position of heterogeneous slab
slab = zeros(Nx, Ny);
r = 22*scale;
a = Nx/2;
b = Ny/2;
for i = a-r+1: a+r
y1 = b - sqrt(r^2 - (i-a)^2); % == (i-(a-r))
y2 = b + sqrt(r^2 - (i-a)^2); % == (i-(a-r))
slab(i, floor(y1): floor(y2)) = 1;
end
% slab(Nx/2:3*Nx/4, Nx/2:3*Nx/4) = 1;
% define the source properties
source_freq = 5e6; % [Hz]
source_strength = 1e3; % [Pa]
source_cycles = 5; % number of tone burst cycles
for j = 3: 3
% === Transmisor TX
TX = zeros(Nx, Ny);
dT = 24*scale;
aT = 0; % 5
% === Distancias para dx
dxT = [ (Nx/2) - r - dT; % ==== Máximo a la izquierda
(Nx/2) - (r/2) - dT; % ==== Medio a la izquierda
(Nx/2) - dT/2; % ==== Centro
(Nx/2) + (r/2); % ==== Medio a la derecha
(Nx/2) + r ]; % ==== Máximo a la derecha
dy = (Ny/2) - 80*scale;
TX(dy-aT: dy, dxT(j): dxT(j) + dT) = 1;
% source_mask = zeros(Nx, Ny);
source_mask = TX;
% define the sensor to record the maximum particle velocity everywhere
% sensor.record = {'u_max_all'};
sensor.record = {'p', 'p_final', 'p_max', 'u_max_all'};
% === Receptor RX
RX = zeros(Nx, Ny);
dxR = [ (Nx/2) - r - dT ; % ==== Máximo a la izquierda
(Nx/2) - (r/2) - dT ; % ==== Medio a la izquierda
(Nx/2) - dT/2 ; % ==== Centro
(Nx/2) + (r/2) ; % ==== Medio a la derecha
(Nx/2) + r ];% ==== Máximo a la derecha
dy = (Ny/2) + 80*scale;
RX(dy: dy+aT, dxR(j): dxR(j) + dT) = 1;
sensor.mask =(RX); % =====
% sensor.record = {'p', 'p_final', 'p_max', 'u_max_all'};
% set the input arguments
input_args = {'PMLSize', PML_size, 'PMLAlpha', 2, 'PlotPML', false, ...
'PMLInside', false, 'PlotScale', [-1, 1]*source_strength, ...
'DisplayMask', 'off', 'DataCast', 'single'};
% =========================================================================
% ELASTIC SIMULATION
% =========================================================================
% define the medium properties
clear medium
medium.sound_speed_compression = cp1*ones(Nx, Ny);
medium.sound_speed_compression(slab == 1) = cp2;
medium.sound_speed_shear = cs1*ones(Nx, Ny);
medium.sound_speed_shear(slab == 1) = cs2;
medium.density = rho1*ones(Nx, Ny);
medium.density(slab == 1) = rho2;
medium.alpha_coeff_compression = alpha0_p1*ones(Nx, Ny);
medium.alpha_coeff_compression(slab == 1) = alpha0_p2;
medium.alpha_coeff_shear = alpha0_s1*ones(Nx, Ny);
medium.alpha_coeff_shear(slab == 1) = alpha0_s2;
% assign the source
clear source
source.s_mask = source_mask;
% source.p0 = -source_strength*toneBurst(1/kgrid.dt, source_freq, source_cycles);
source.sxx = source_strength*toneBurst(1/kgrid.dt, source_freq, source_cycles);
source.syy = source.sxx;
source.s_mode = 'dirichlet';
clear sensor
sensor.mask =(RX);
sensor.record = {'p', 'p_final', 'p_max', 'u_max_all', 'p_max_all'};
% run the elastic simulation
sensor_data_elastic = pstdElastic2D(kgrid, medium, source, sensor, input_args{:});
% =========================================================================
% VISUALISATION
% =========================================================================
% define plot vector
x_vec = kgrid.x_vec(1 + PML_size:end - PML_size)*1e3;
y_vec = kgrid.y_vec(1 + PML_size:end - PML_size)*1e3;
% calculate square of velocity magnitude
u_e = sensor_data_elastic.ux_max_all.^2 + sensor_data_elastic.uy_max_all.^2;
% u_f = sensor_data_fluid.ux_max_all.^2 + sensor_data_fluid.uy_max_all.^2;
figure(5)
imagesc(y_vec, x_vec, 20*log10(u_e./max(u_e(:))));
xlabel('y [mm]');
ylabel('x [mm]');
axis image;
colorbar;
caxis([-50, 0]);
title('Elastic Model');
colormap(jet(256));
% === Gráfica de la señal recibida
SDE{1} = zeros(1, size(sensor_data_elastic.p, 2));
for i = 1: size(sensor_data_elastic.p, 2)
SDE{j}(i) = sum(sensor_data_elastic.p(:, i))/size(sensor_data_elastic.p, 1);
end
figure(12)
set(gca, 'nextplot', 'replacechildren', 'FontSize', 14)
plot(kgrid.t_array, SDE{j}, 'r-');
xlabel('Time [s]');
ylabel('Signal Amplitude');
axis([kgrid.t_array(1) kgrid.t_array(end) min(SDE{j})*1.2 max(SDE{j})*1.2])
title('Sensor Pressure Signal');
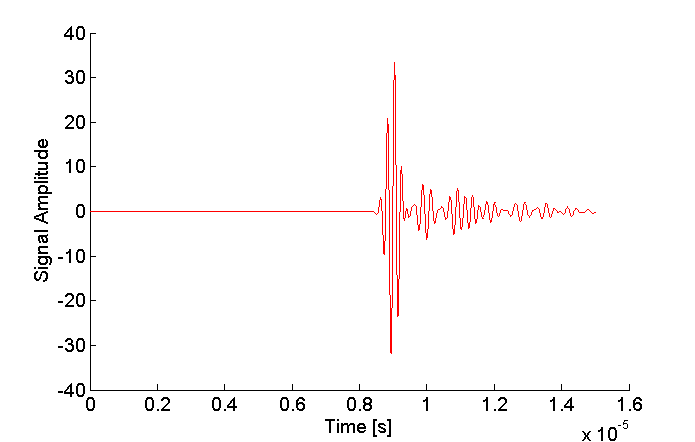
endAfter running the simulation i obtain a signal like this one:
I cannot identify that signal, i have no idea what it is. If some one could help me out and tell me what i am looking at would deeply appreciate it.
Thanks in advanced.
Rodrigo