Large-Scale Ultrasound Simulations with Local Fourier Basis Decomposition (Supercomputing 2015)

Jiri Jaros (Brno University of Technology), Matej Dohnal (Brno University of Technology), Bradley Treeby (University College London)

Download Two Page Extended Abstract
Download Poster

Overview

The simulation of ultrasound wave propagation through biological tissue has a wide range of practical applications including planning therapeutic ultrasound treatments. The major challenge is to ensure the ultrasound focus is accurately placed at the desired target since the surrounding tissue can significantly distort it (see below for an animation of a plane wave propagating through the femoral neck using data from this paper). Performing accurate ultrasound simulations, however, requires the simulation code to be able to exploit thousands of processor cores to deliver simulation results within 24 hours. Our existing code (described in this paper) uses the pseudospectral time domain method (PSTD) to achieve high accuracy. However, this is based on performing 3D fast Fourier transforms (FFT) which introduces global all-to-all communications that are a major performance bottleneck.

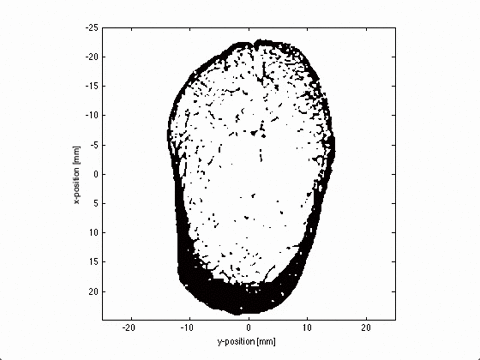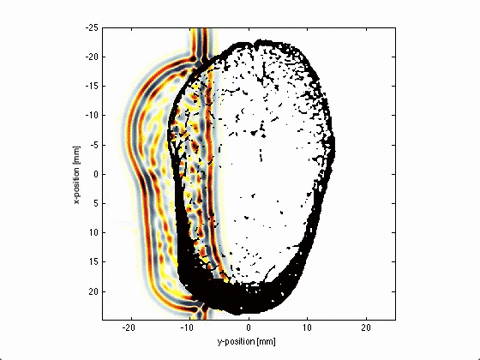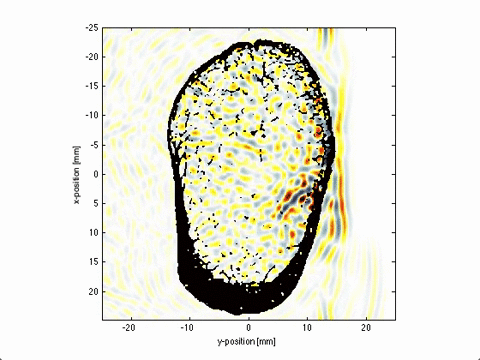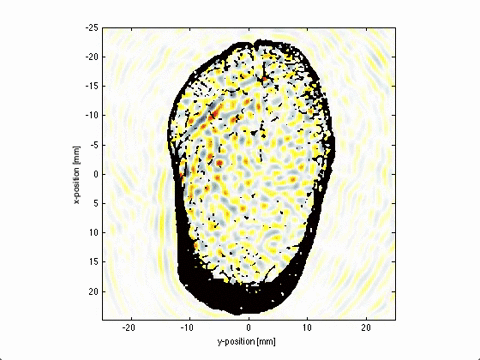
Local Domain Decomposition

This poster presents a novel domain decomposition method for the PSTD method based on local Fourier basis. The global domain is divided into local subdomains which run independent simulations (i.e., gradients are performed using local, rather than global, Fourier basis functions). To maintain spectral accuracy, the field variables on each of the local subdomains are multiplied by a bell function which forces the data to be periodic.

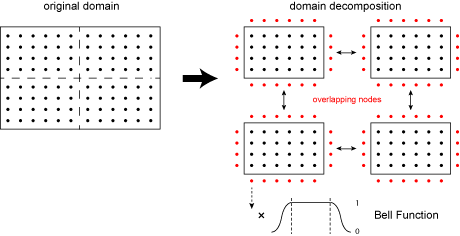
At the end of each time step, local data is exchanged between neighbouring subdomains. This reduces communication overhead introduced by the FFT by replacing the global all-to-all communications with local nearest-neighbour communication patterns. An example is shown below, where the global domain is divided into 8 subdomains which run independent simulations, with local data exchange at the end of each time step.

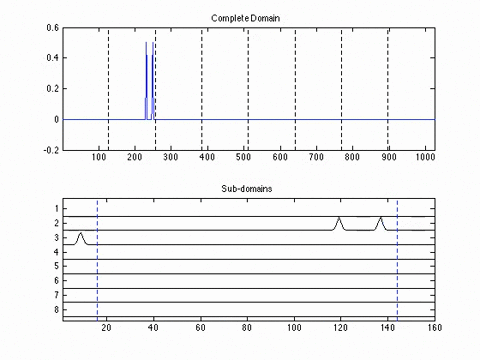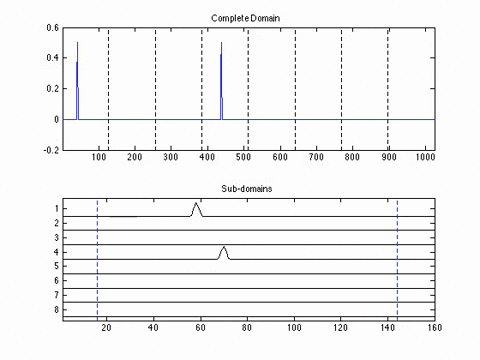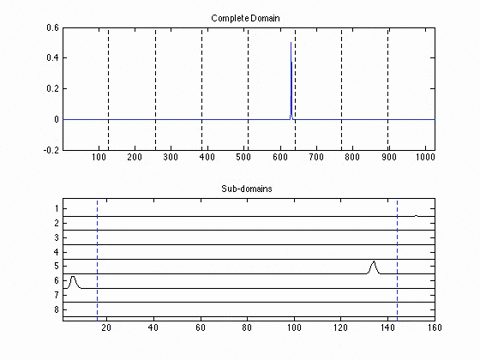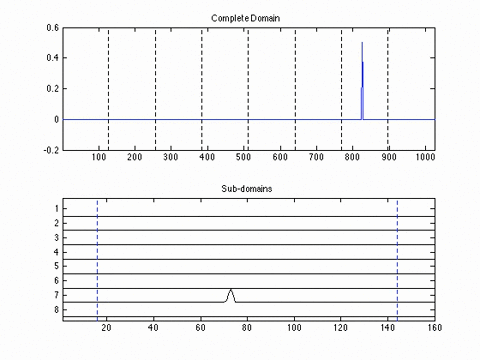
Experimental Results

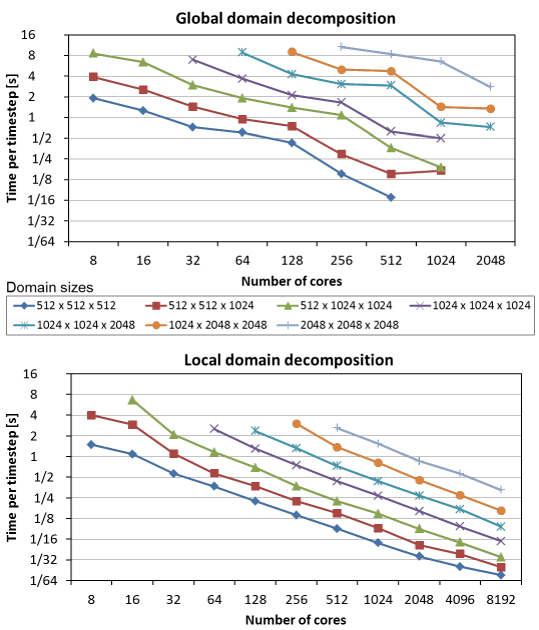
The performance and scaling were investigated using spatial grid sizes between 512^3 and 2048^3 grid points. We used the thin nodes on the SuperMUC cluster (two 8-core Sandy Bridges) and scaled the calculation from 8 cores (one socket) to 8192 cores (512 nodes). The figure below illustrates strong scaling results for global domain decomposition (GDD; our previous code) and local domain decomposition (LDD). The scaling of GDD is limited and shows significant performance fluctuations dependent on the domain size (this is due to the communication strategy used, which is discussed in more detail here). Conversely, LDD scales up to 8192 cores for all domain sizes. Moreover, the scaling curves for LDD are smoother and steeper yielding much higher efficiency. The shape of the scaling curves suggests that large domains will be easy to scale to even higher number of cores.

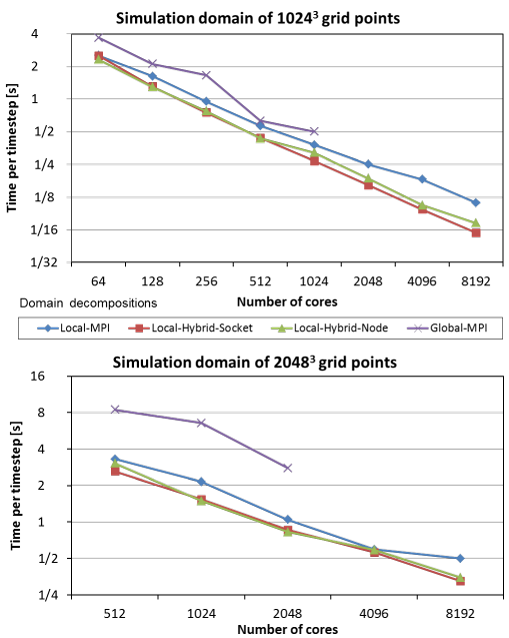
The figure below directly compares GDD and three types of LDD (pure-MPI version, and hybrid OpenMP/MPI versions with a single process per socket and per node). The hybrid versions further reduce communication overhead and the relative size of the halo region. This leads to superior performance of both hybrid versions which can outperform the pure-MPI and GDD versions on the same number of cores by a factor of 1.5 and 4, respectively.

Summary

This poster has presented a novel domain decomposition for spectral methods based on local Fourier basis allowing up to 16 times more computer cores to be employed. The time per simulation timestep was reduced by a factor of 8.55 in the best case. Since very large-scale ultrasound simulations (>2048^3) often need a week to finish on 1024 cores, this decomposition can reduce simulations below 24 hours, which is a more clinically meaningful timeframe.